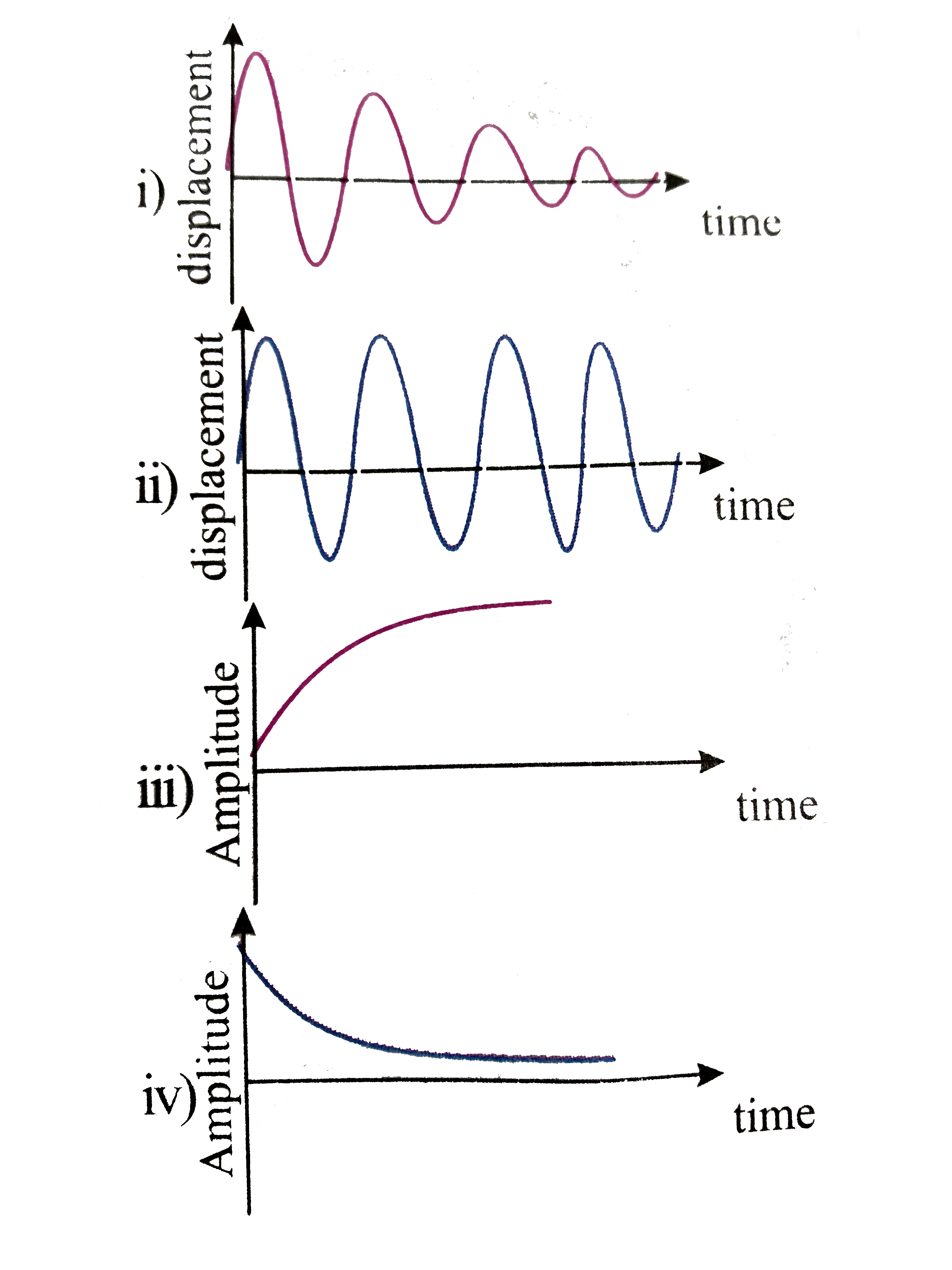
Oscillation Damped Harmonic Motion . Critical damping returns the system to equilibrium as. a clock escapement is a device that can transform continuous movement into discrete movements of a gear train. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to describe this more general case. damping oscillatory motion is important in many systems, and the ability to control the damping is even more so. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. if the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by \[n=[\gamma \tau / 2 \pi] \simeq\left[(k / m)^{1 / 2}(m / \pi b)\right]=\left[\omega_{0}(m / \pi b)\right] \nonumber \] A guitar string stops oscillating a few seconds after being plucked.
from ar.inspiredpencil.com
if the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by \[n=[\gamma \tau / 2 \pi] \simeq\left[(k / m)^{1 / 2}(m / \pi b)\right]=\left[\omega_{0}(m / \pi b)\right] \nonumber \] A guitar string stops oscillating a few seconds after being plucked. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. Critical damping returns the system to equilibrium as. a clock escapement is a device that can transform continuous movement into discrete movements of a gear train. damping oscillatory motion is important in many systems, and the ability to control the damping is even more so. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to describe this more general case.
Damped Harmonic Oscillator Examples
Oscillation Damped Harmonic Motion A guitar string stops oscillating a few seconds after being plucked. a clock escapement is a device that can transform continuous movement into discrete movements of a gear train. Critical damping returns the system to equilibrium as. A guitar string stops oscillating a few seconds after being plucked. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to describe this more general case. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. damping oscillatory motion is important in many systems, and the ability to control the damping is even more so. if the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by \[n=[\gamma \tau / 2 \pi] \simeq\left[(k / m)^{1 / 2}(m / \pi b)\right]=\left[\omega_{0}(m / \pi b)\right] \nonumber \]
From exounhfkb.blob.core.windows.net
Damped Harmonic Oscillator Equation at Hannah Sullivan blog Oscillation Damped Harmonic Motion Critical damping returns the system to equilibrium as. A guitar string stops oscillating a few seconds after being plucked. if the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by \[n=[\gamma \tau / 2 \pi] \simeq\left[(k / m)^{1 / 2}(m / \pi b)\right]=\left[\omega_{0}(m / \pi b)\right]. Oscillation Damped Harmonic Motion.
From www.slideserve.com
PPT Chapter 14 Oscillations PowerPoint Presentation, free download Oscillation Damped Harmonic Motion if the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by \[n=[\gamma \tau / 2 \pi] \simeq\left[(k / m)^{1 / 2}(m / \pi b)\right]=\left[\omega_{0}(m / \pi b)\right] \nonumber \] a clock escapement is a device that can transform continuous movement into discrete movements of a. Oscillation Damped Harmonic Motion.
From animalia-life.club
Damped Harmonic Oscillator Examples Oscillation Damped Harmonic Motion A guitar string stops oscillating a few seconds after being plucked. Critical damping returns the system to equilibrium as. damping oscillatory motion is important in many systems, and the ability to control the damping is even more so. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion. Oscillation Damped Harmonic Motion.
From www.youtube.com
Damped Oscillation Damped Harmonic Motion Amplitude and Energy of Oscillation Damped Harmonic Motion a clock escapement is a device that can transform continuous movement into discrete movements of a gear train. if the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by \[n=[\gamma \tau / 2 \pi] \simeq\left[(k / m)^{1 / 2}(m / \pi b)\right]=\left[\omega_{0}(m / \pi b)\right]. Oscillation Damped Harmonic Motion.
From www.youtube.com
damped harmonic motion equation of damped harmonic oscillations with Oscillation Damped Harmonic Motion a clock escapement is a device that can transform continuous movement into discrete movements of a gear train. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. damping oscillatory motion is important in many systems, and the ability to control the damping is even more. Oscillation Damped Harmonic Motion.
From www.slideserve.com
PPT Chapter 13 Oscillatory Motions PowerPoint Presentation, free Oscillation Damped Harmonic Motion Critical damping returns the system to equilibrium as. damping oscillatory motion is important in many systems, and the ability to control the damping is even more so. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. in this section, we examine some examples of damped. Oscillation Damped Harmonic Motion.
From mungfali.com
Damped Harmonic Motion Oscillation Damped Harmonic Motion A guitar string stops oscillating a few seconds after being plucked. Critical damping returns the system to equilibrium as. a clock escapement is a device that can transform continuous movement into discrete movements of a gear train. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. Oscillation Damped Harmonic Motion.
From www.youtube.com
Solving the Damped Harmonic Oscillator YouTube Oscillation Damped Harmonic Motion in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to describe this more general case. damping oscillatory motion is important in many systems, and the ability to control the damping is even more so. a clock escapement is a device that can transform continuous movement into. Oscillation Damped Harmonic Motion.
From www.youtube.com
Damped Harmonic Oscillators Derivation YouTube Oscillation Damped Harmonic Motion A guitar string stops oscillating a few seconds after being plucked. damping oscillatory motion is important in many systems, and the ability to control the damping is even more so. a clock escapement is a device that can transform continuous movement into discrete movements of a gear train. in this section, we examine some examples of damped. Oscillation Damped Harmonic Motion.
From www.vernier.com
Damped Harmonic Motion Oscillation Damped Harmonic Motion if the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by \[n=[\gamma \tau / 2 \pi] \simeq\left[(k / m)^{1 / 2}(m / \pi b)\right]=\left[\omega_{0}(m / \pi b)\right] \nonumber \] a clock escapement is a device that can transform continuous movement into discrete movements of a. Oscillation Damped Harmonic Motion.
From www.slideserve.com
PPT Damped Harmonic Motion PowerPoint Presentation, free download Oscillation Damped Harmonic Motion damping oscillatory motion is important in many systems, and the ability to control the damping is even more so. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to describe this more general case. Critical damping returns the system to equilibrium as. if the system is. Oscillation Damped Harmonic Motion.
From www.slideserve.com
PPT Chapter 14 Oscillations PowerPoint Presentation, free download Oscillation Damped Harmonic Motion in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. a clock escapement is a device that can transform continuous movement into discrete movements of a gear train. in this section, we examine some examples of damped harmonic motion and see how to modify the equations. Oscillation Damped Harmonic Motion.
From www.toppr.com
Damped Simple Harmonic Motion Definition, Expression, Example, Video Oscillation Damped Harmonic Motion damping oscillatory motion is important in many systems, and the ability to control the damping is even more so. A guitar string stops oscillating a few seconds after being plucked. if the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by \[n=[\gamma \tau / 2. Oscillation Damped Harmonic Motion.
From www.slideserve.com
PPT Chapter 11 Oscillations and Waves PowerPoint Presentation, free Oscillation Damped Harmonic Motion in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to describe this more general case. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. a clock escapement is a device that can transform continuous. Oscillation Damped Harmonic Motion.
From ppt-online.org
Oscillatory motion. Simple harmonic motion. The simple pendulum. Damped Oscillation Damped Harmonic Motion in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. A guitar string stops oscillating a few seconds after being plucked. if the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by \[n=[\gamma \tau. Oscillation Damped Harmonic Motion.
From cityraven.com
😀 Example of damped harmonic motion. What are some examples of simple Oscillation Damped Harmonic Motion a clock escapement is a device that can transform continuous movement into discrete movements of a gear train. Critical damping returns the system to equilibrium as. if the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by \[n=[\gamma \tau / 2 \pi] \simeq\left[(k / m)^{1. Oscillation Damped Harmonic Motion.
From studylib.net
Damped Simple Harmonic Motion Oscillation Damped Harmonic Motion Critical damping returns the system to equilibrium as. damping oscillatory motion is important in many systems, and the ability to control the damping is even more so. if the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by \[n=[\gamma \tau / 2 \pi] \simeq\left[(k /. Oscillation Damped Harmonic Motion.
From www.toppr.com
The equation of a damped simple harmonic motion is md^2x/dt^2 + bdx/dt Oscillation Damped Harmonic Motion in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to describe this more general case. if the system is very weakly damped, such that \((b / m)^{2}<<4 k / m\), then we can approximate the number of cycles by \[n=[\gamma \tau / 2 \pi] \simeq\left[(k / m)^{1. Oscillation Damped Harmonic Motion.